I know that this is a standard results. But a hands on proof is really useful because it makes things more clear. I knew the fact that any permutation could be broken into disjoint cycles. However I did not know how the sign of the permutation changes if we swap the elements with in a disjoint cycle. It turns out that some of the fundamental properties of the signs of the permutation can be used to prove the sufficiency of a perfect matching in graph. A Tutte Matrix is defined as follows.
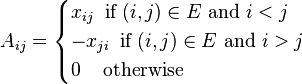
Given a Tutte matrix we now prove the sufficiency of perfect matching
Determinant of Tutte matrix is as follows- PROPERTY-1 If
 is a cycle
in
is a cycle
in  then if we replace
then if we replace 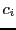 with reverse cycle
with reverse cycle
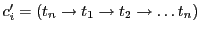 then
then 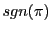 remains
the same - because we did not change the number of swaps required but just changed the order of swaps. For instance,
let
remains
the same - because we did not change the number of swaps required but just changed the order of swaps. For instance,
let
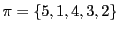 then cycle
then cycle
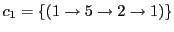 now we replace
it with
now we replace
it with
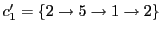 . This results in
. This results in
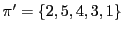 .
.
- PROPERTY-2 Let
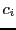 is a cycle of odd length in
is a cycle of odd length in  and let
and let 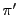 be the permutation
by replacing
be the permutation
by replacing 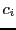 with its reverse cycle
with its reverse cycle 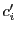 . Then the corresponding terms in the determinant
for
. Then the corresponding terms in the determinant
for 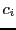 and
and 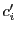 are
are
 and
and
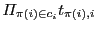 .
For example in the previous example
.
For example in the previous example
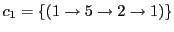 so the
corresponding term in the determinant for
so the
corresponding term in the determinant for  is
is
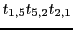 . On the other hand
the reverse cycle
. On the other hand
the reverse cycle
 has the following term
has the following term
 in the determinant.
in the determinant.
- PROPERTY-3 If all the cycles in the permutation
 are even and corresponding term
in the determinant (i.e.
are even and corresponding term
in the determinant (i.e.
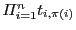 ) is non-zero then its the set
) is non-zero then its the set
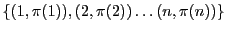 is a valid perfect match in the graph. This is because by the definition of Tutte matrix
is a valid perfect match in the graph. This is because by the definition of Tutte matrix
 represents an edge in the graph and the permutation
represents an edge in the graph and the permutation  is giving a subset of
is giving a subset of  edges since
the product is non-zero, on the other than this sub-set of edges is a match.
edges since
the product is non-zero, on the other than this sub-set of edges is a match.
No comments:
Post a Comment