De Bruijn graphs recently found applications in
Sequence Assembly(
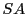
).
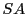
problem is close to
Shortest Common super String(
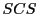
) problem, however
there are some fundamental differences. Given a set of input strings

strings the
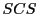
problem outputs a string

such that every
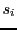
is a sub-string in

and

. On the other hand the input to the
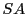
problem
is a set
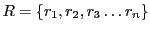
of strings, every

is a randomly chosen
sub-string of a bigger string

- called the
genome. Unfortunately we do not
know what

is, so given
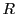
the
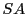
problem asks to find the

such that we can
explain every

. Adding to the complexity of
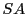
problem

may contain several
repeating regions and the direct appliction of
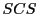
to solve
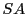
problem would
result in collapsing the repeating regions in

- so we cannot directly reduce
the
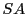
problem to
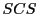
. Also the string

is special string coming from the
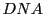
so its double stranded and each

may be originating from the forward or
reverse compliments of

.
![\includegraphics[scale=0.5]{loops_debrujin.eps}](http://vamsi99.users.sourceforge.net/blg/LOOP-2009/img19.png)
A  De Bruijn graph
De Bruijn graph  on a set of strings
on a set of strings 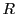 is a graph whose vertices
correspond to the unique
is a graph whose vertices
correspond to the unique  mers (a string of length
mers (a string of length 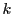 ) from all the
) from all the 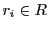 and whose edges correspond to a some
and whose edges correspond to a some  mer in some
mer in some  . Also to consider
the double stranded-ness we also include a reverse compliment of every
. Also to consider
the double stranded-ness we also include a reverse compliment of every  mer into
the graph
mer into
the graph  . In the following simple example I show how a loop (i.e. both
the forward and reverse compliments overlapping each other by
. In the following simple example I show how a loop (i.e. both
the forward and reverse compliments overlapping each other by  ) can originate
into
) can originate
into  . This interesting situation seems to be referred to as hairpin-loop.
. This interesting situation seems to be referred to as hairpin-loop.
![\includegraphics[scale=0.5]{loops_debrujin.eps}](http://vamsi99.users.sourceforge.net/blg/LOOP-2009/img19.png)
![]() De Bruijn graph
De Bruijn graph ![]() on a set of strings
on a set of strings ![]() is a graph whose vertices
correspond to the unique
is a graph whose vertices
correspond to the unique ![]() mers (a string of length
mers (a string of length ![]() ) from all the
) from all the ![]() and whose edges correspond to a some
and whose edges correspond to a some ![]() mer in some
mer in some ![]() . Also to consider
the double stranded-ness we also include a reverse compliment of every
. Also to consider
the double stranded-ness we also include a reverse compliment of every ![]() mer into
the graph
mer into
the graph ![]() . In the following simple example I show how a loop (i.e. both
the forward and reverse compliments overlapping each other by
. In the following simple example I show how a loop (i.e. both
the forward and reverse compliments overlapping each other by ![]() ) can originate
into
) can originate
into ![]() . This interesting situation seems to be referred to as hairpin-loop.
. This interesting situation seems to be referred to as hairpin-loop.
No comments:
Post a Comment