![\begin{theorem}
Let $A$,$B$\ and $C$\ be three $n\times n$\ matrices such that $...
...tribution. Then $P[AB\vec{r} = C\vec{r} \vert AB \neq C] \leq 1/2$
\end{theorem}](http://vamsi99.users.sourceforge.net/blg/RAND-2009/img20.png)
Proof.
Let  be a
be a 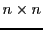 matrix and
matrix and
 be the column vectors of
be the column vectors of  .
Then
.
Then
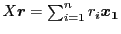 . This means that multiplying a vector with a matrix is linear
combination of the columns, the coefficient
. This means that multiplying a vector with a matrix is linear
combination of the columns, the coefficient 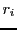 is the
is the 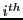 component of
component of 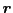 . Since
. Since 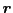 is a boolean and
is a boolean and 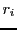 acts as an indicator variable on the selection of column
acts as an indicator variable on the selection of column 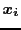 . So if
. So if 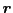 is chosen from a uniform distribution
is chosen from a uniform distribution
![$ P[r_i=0] = P[r_i=1] = 1/2$](http://vamsi99.users.sourceforge.net/blg/RAND-2009/img29.png) .
.
Now let ![]() and
and
![]() be the column vectors of
be the column vectors of ![]() , similarly
let
, similarly
let
![]() be the column vectors of
be the column vectors of ![]() . Let
. Let
![]() , clearly
, clearly
![]() since
since ![]() . Then
. Then
![]() since
since
![]() . Intuitively this means we select our random vector
. Intuitively this means we select our random vector ![]() such that
such that
![]() for all
for all ![]() , such a selection will always ensure
, such a selection will always ensure
![]() even though
even though
![]() .
.
![]()
![]()
No comments:
Post a Comment