So coming back to our original problem given the modulo-![]() representation
representation ![]() , we would
like to round
, we would
like to round ![]() to
to ![]() , where
, where ![]() is the smallest multiple of
is the smallest multiple of ![]() such that
such that ![]() .
To accomplish this task we need to examine the first (from right)
.
To accomplish this task we need to examine the first (from right) ![]() digits in the modulo-
digits in the modulo-![]() representation of
representation of ![]() . In fact the value of in those
. In fact the value of in those ![]() bits is the reminder we get when we
divide
bits is the reminder we get when we
divide ![]() by
by ![]() , so if
, so if ![]() is the value in those
is the value in those ![]() bits then
bits then
![]() . When
. When
![]() we can elegantly use the bit-wise operators to accomplish this. So if some one gives
an integer
we can elegantly use the bit-wise operators to accomplish this. So if some one gives
an integer ![]() and ask to find a smallest
and ask to find a smallest ![]() which is a multiple of
which is a multiple of ![]() then we
use the following C-statement to accomplish this
then we
use the following C-statement to accomplish this
![]() .
Where
.
Where ![]() are the standard bit-wise operators in C.
are the standard bit-wise operators in C.
Algorithms, Theory, Spirituality, Life, Technology, Food and Workout : trying to sort these deterministically in $\Theta(1)$ time (constant time).
Saturday, January 30, 2010
Rounding An Integer To The Next Maximal Mutliple Of A Given Radix Power
Let
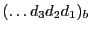 be the modulo-
be the modulo-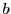 representation of an integer
representation of an integer  , where each
, where each 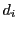 is a symbol/digit corresponding to values
is a symbol/digit corresponding to values
 . Often we are encountered with
problems where we need to find smallest integer
. Often we are encountered with
problems where we need to find smallest integer 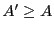 such that
such that  (i.e.
(i.e. 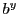 divides
divides 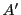 without any reminder), where
without any reminder), where 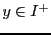 . Some of the very common applications include rounding the number
of bits required to represent a data structure to the nearest byte (i.e. power of
. Some of the very common applications include rounding the number
of bits required to represent a data structure to the nearest byte (i.e. power of 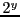 ).
Before we see how to address this problem its worth while to understand the following interesting property of
modulo representation. Given a modulo-
).
Before we see how to address this problem its worth while to understand the following interesting property of
modulo representation. Given a modulo-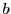 representation of
representation of  we can get corresponding modulo-
we can get corresponding modulo-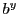 representation of
representation of  by replacing every group of
by replacing every group of 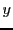 digits (in modulo-
digits (in modulo-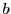 representation), by the
corresponding digit (i.e.
representation), by the
corresponding digit (i.e.
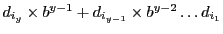 ) in modulo-
) in modulo-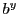 .
For instance if we would like to convert an integer
.
For instance if we would like to convert an integer  in binary (i.e.
in binary (i.e. 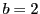 ) representation to hexa-decimal
representation (
) representation to hexa-decimal
representation ( ). We start from left to right and replace every
). We start from left to right and replace every  bits with the corresponding
digit in hexa-decimal system. For example if we see
bits with the corresponding
digit in hexa-decimal system. For example if we see 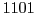 we will replace it with digit
we will replace it with digit 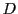 ,
, 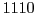 by
by
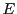 and so on. So the hexa-decimal system is providing us with a one-one function
and so on. So the hexa-decimal system is providing us with a one-one function
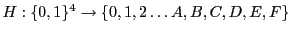 for every
for every  bit string, in fact we can use any
one-one function here when we move for modulo
bit string, in fact we can use any
one-one function here when we move for modulo 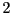 representation to modulo
representation to modulo  . However the one-one
function
. However the one-one
function 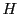 has become a standard for module
has become a standard for module  system.
system.
Subscribe to:
Post Comments (Atom)
No comments:
Post a Comment